I’m not sure why I haven’t noticed the esoteric study of Medieval Geomancy before. There are 16 figures, each having four vertical binary digits of one or two dots, and there are several relationships between the figures, as well as arcane meanings. And there are quite a few introductions to the subject on the web, like many other occult topics have.
I’m not sure why I haven’t noticed the esoteric study of Medieval Geomancy before. There are 16 figures, each having four vertical binary digits of one or two dots, and there are several relationships between the figures, as well as arcane meanings. And there are quite a few introductions to the subject on the web, like many other occult topics have.
The figures are as follows (with the number explained below):
0 Populus (People)
1 Laetitia (Joy)
2 Rubeus (Red)
3 Fortuna Minor (Lesser)
4 Albus (White)
5 Amissio (Loss)
6 Conjunctio (Union)
7 Cauda Draconis (Head)
8 Tristitia (Sorrow)
9 Carcer (Prison)
A Acquisitio (Gain)
B Puer (Boy)
C Fortuna Major (Greater)
D Puella (Girl)
E Caput Draconis (Tail)
F Via (Path)
I think I have numbered them in reverse of what is usual, because to me it seemed that the top line Fire to be the most mobile, then Air, then Water, and then Earth to be the least. Thus Fire should change most frequently, and so on. A line with two dots is usually thought of as passive (0), and one dot is active (1).
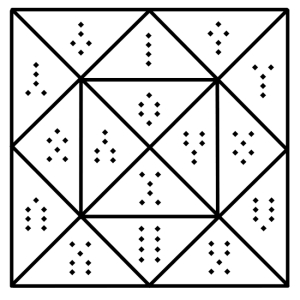
And so I have numbered the 16 figures as a hexadecimal digit where Fire is in the one’s place, Air is in the two’s place, Water is in the four’s place, and Earth is in the eight’s place. For example, Puella is 1101 or D (decimal 13).
The arrangement of the figures on the diagram above has the so called Reversion of each being the one reflected through a vertical mirror, and the Inversion of each being the one reflected about the center point of the diagram. For example, the Reversion of Puella is Puer, and the Inversion of Puella is Rebeus.
There is also the operation of Conversion, or a combination of both Inversion and Reversion. Those associated figures are found via a horizontal mirror through the center point. Note also what are called the entering figures are on the right side, the exiting figures are on the left side, and the ones along the center are both entering and exiting.
Finally, I couldn’t resist showing the figures as their dotted glyphs, but with them all oriented correctly (i.e. vertically). The diagram is more or less the same as the arrangement found in Four Forms Make a Universe, Part 2.
https://en.m.wikipedia.org/wiki/Geomantic_figures
https://en.m.wikipedia.org/wiki/Geomancy
https://www.princeton.edu/~ezb/geomancy/figures.html
https://www.princeton.edu/~ezb/geomancy/geostep.html
https://www.princeton.edu/~ezb/geomancy/agrippa.html
http://www.quadibloc.com/other/geoint.htm
https://digitalambler.com/category/geomancy/
<>