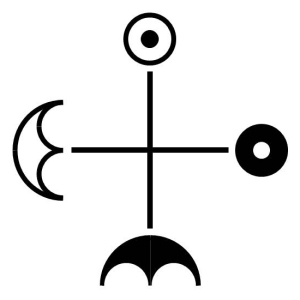
In addition to the symbolic fourfold presented in the previous entry Fourfolds and Double Duals, which includes the alchemical symbols for the four elements, here is another generic representation. This fourfold reminds me of the fourfolds Bright-Light-Dim-Dark shown in the early entry with the Four Elements, as well as the newer fourfold of The One and the Many.
If one considers the outer ring and the inner circle to be “outer-as-inner”, then this fourfold is related to the One and the Many by letting One be white and Many be black.
Additionally, the symbols can be seen to map to the fourfold Bright-Light-Dim-Dark by noting that White-as-White is Bright, White-as-Black is Light, Black-as-White is Dim, and Black-as-Black is Dark.
For fun, this figure can be tweaked to reveal a deconstructed yin yang. It reminds me of John Dee’s Hieroglyphic Monad. Or someone holding a Vulcan Lirpa from Star Trek’s Amok Time.
References:
http://en.wikipedia.org/wiki/Monas_Hieroglyphica
Notes:
Amusingly, I’m starting to think of the lower figure as a crossed fork and spoon: a fork to separate and a spoon to combine. Note the handles of the utensils (the circles) appear to be switched, but that is just the way it is.
Also: a c & t’s mouth and c ⅋ t’s eye; a d ⊕ g’s nose and d ⊗ g’s eye. These are the binary operators of Linear Logic!
<>
Equivalent eXchange 