Here is another example of a fourfold, in the mathematics of Fourier Analysis. Here the four elements of our investigation resolve into Discrete Time, Continuous Time, the Fourier Series, and the Fourier Transform.

From the three dualities of Time – Frequency, Periodic – Aperiodic, and Discrete – Continuous, we obtain the four combinations Discrete Time/Periodic Frequency, Continuous Time/Aperiodic Frequency, the Fourier Series (Periodic Time/Discrete Frequency), and the Fourier Transform (Aperiodic Time/Continuous Frequency).

In the table below, T stands for Time and f for Frequency. The subscripts denote the attributes of each: D for Discrete, C for Continuous, P for Periodic, and A for Aperiodic. So T subscript C, f subscript A means that when Time is Continuous, Frequency is Aperiodic, etc. Please see Steve Tjoa’s web site for the equations for the Fourier Series and the Fourier Transform in Continuous and Discrete Time.

References:

http://stevetjoa.com/633

http://en.wikipedia.org/wiki/Fourier_analysis

http://en.wikipedia.org/wiki/Fourier_series

http://en.wikipedia.org/wiki/Fourier_transform

[*7.74, *7.108]

evolution, fourfolds, Science

The Theory of Evolution

June 8, 2012 Martin K. Jones 2 Comments

“I have called this principle, by which each slight variation, if useful, is preserved, by the term Natural Selection”

— Charles Darwin

Can we cast the theory of evolution into a fourfold? I propose that the following four processes can serve as an abstract model for evolution: generation, variation, speciation, and selection. These four entities are similar to the fourfold of Structure-Function, currently in development. By my analogy which will be explained later, Generation is action, Variation is part, Speciation is structure, and Selection is function. A more familiar analogy matches these four processes to Aristotle’s Four Causes: Generation is efficient cause, Variation is material cause, Speciation is formal cause, and Selection is final cause.

Generation: Offspring are like their parents by and large, except when made different by processes of variation. Mainly the act of reproduction, procreation, or replication, but includes the ordinary evolutionary factors of descent and heredity.

Variation: Offspring can be different than parents. Includes the factors of genetic variation, mutation, sexual reproduction, and genetic drift.

Speciation: Includes the factors which keep species separated and differentiated from each other.

Selection: Really natural selection. I always thought this was a negative process, where species become extinct or are selected out if they are ill adapted to their environment. Apparently the original meaning was that the fittest organisms and their traits continue: that is, they are selected to survive by nature because of their adaptive traits.

As a process of change, evolution has been suggested by scientists to operate at many levels of nature, not just for the biological. One such scientist is Eric Chaisson, who has written many books on his idea of “cosmic evolution”.

References:

http://en.wikipedia.org/wiki/Evolution

http://en.wikipedia.org/wiki/Reproduction

http://en.wikipedia.org/wiki/Genetic_variation

http://en.wikipedia.org/wiki/Speciation

http://en.wikipedia.org/wiki/Natural_selection

https://www.cfa.harvard.edu/~ejchaisson/cosmic_evolution/docs/splash.html

Eric Chaisson / Epic of Evolution: seven ages of the cosmos (2005)

Note:

Also note the similarity between this fourfold and the fourfold I have drawn for Kevin Kelly’s Philosophy of Technology. In “What Technology Wants”, Kelly claims that technology develops in an evolutionary manner.

[*7.96]

fourfolds, logic

The Square of Opposition

May 21, 2012 Martin K. Jones 3 Comments

Some readers may think I’ve never met a fourfold I didn’t like. However, there are several that I haven’t presented here because they don’t seem to play well with the others. The Square of Opposition, created by Aristotle, is one such fourfold. The four logical forms of the square are relations between a subject and predicate, S and P, and supposedly exhaust the possibilities of belonging: Some S are P, Some S are not P, All S are P, and No S are P (or All S are not P).

In the diagram I have removed the S and P, and the logical forms become spare and like a Zen Koan or nursery rhyme: Some Are, Some Are Not, All Are, and None Are (or All Are Not). By doing so, they resonate more brightly with the other fourfolds and how they are presented herein. Now, the logical forms can be about existence, or the subject and predicate withdraw and become implicit to the thought.

Note:

Compare and contrast the Square of Opposition to the Tetralemma and the Semiotic Square.

The 3rd World Congress on the Square of Opposition is soon to convene. May the meeting be rewarding!

References:

http://en.wikipedia.org/wiki/Square_of_opposition

http://plato.stanford.edu/entries/square

http://www.iep.utm.edu/sqr-opp/

http://www.square-of-opposition.org/

[*4.84, *5.82, *7.70, *7.90]

fourfolds, Physics, Science

Attraction and Repulsion

May 11, 2012 Martin K. Jones 2 Comments

Gravity is Love.

— Brian Swimme

The principle of attraction and its opposite repulsion is pervasive throughout the conceptualization of modern physics. Even ancient Empedocles, of the four elements fame, thought that in all nature the force of attraction and combination was Love or Philia, and that the force of repulsion and separation was Strife or Neikos. These forces have now been depersonalized and mathematized, but still inhabit natural laws which must be obeyed. (See the Four Fundamental Forces of Physics.)

At all levels of matter and energy, from the lowest atomic interactions to the highest cosmic forces, the duality of attraction and repulsion are everywhere. In atoms, there is the strong force and the weak force that respectively pull nuclei together or push them apart. In and between atoms and molecules, covalent bonds, magnetic polarities, electric charges, hydrogen bonds, salt bridges, and hydrophobic effects gather and scatter and even make life possible. In the large-scale macro world, electromagnetism and gravity extend their influence. And in the cosmic arena, the mysterious effects of dark matter and dark energy perform without our current understanding.

In the biological world, attraction and repulsion are seen in the action of plants and animals. The plant is attracted to light and moisture, and repulsed by darkness and dryness. The animal is attracted to food and safety, and repulsed by lack and danger. Plants and animals are also attracted to their kin, and repulsed by their non-kin, because there is strength in commonality. However, too much sameness becomes toxic. It is the dynamic between attraction and repulsion that creates much of the living world and its richness.

In the human world, culture and language enable the forces of attraction and repulsion. Known culture and language is attractive; unknown culture and language is repulsive. But the human mind also craves newness. Interactions between the same and the different have been a great source of the creative drive which fuels the human spirit.

Note:

The sums of attractions are combinations. The sums of repulsions are separations.

References:

http://en.wikipedia.org/wiki/Empedocles

http://www.npr.org/blogs/13.7/2010/10/21/130724690/gravity-is-love

[*7.92]

fourfolds

Wu Wei or Natural Action

May 9, 2012 Martin K. Jones 2 Comments

The sage does nothing, and yet everything is done.

— Lao Tzu from Tao te Ching

The principle of least action (or stationary action) seen in the previous entry Noether’s Theorem immediately makes me think of the Taoist concept of wu wei – literally no action or effortless action. It consists of knowing when to act and knowing when not to act (or perhaps even not knowing to act). It also means natural action, or the action of natural physical or biological systems. In Western culture, such action is considered bad and “mechanical” because physical systems are thought to be like clockwork, but in Eastern culture, it is sagelike and enlightened, harmonious. Very often intention, or conscious action, gets in the way and impedes our effort.

Another example that comes to mind is the short story “On the Marionette Theatre” by Heinrich von Kleist. In the story, one of the characters comment that marionettes possess a grace humans do not, a view which contradicts ordinary aesthetics. It is claimed that our consciousness and capacity for reflection cause us to doubt ourselves or become self-conscious, and prevent us from acting with the singlemindedness and purity of an animal or a puppet. For example, a bear in the story is able to successfully fence with the narrator, by deflecting every thrust towards him seemingly without effort. And all feints are ignored, as if the bear is reading the narrator’s mind or knowing the future before it happens.

Also note:

Philip Pullman, author of the fantasy trilogy “His Dark Materials”, was inspired by von Kleist’s story.

The character Forrest Gump, of book and movie fame, could be considered a Taoist. Be like a feather on the wind…

http://en.wikipedia.org/wiki/Wu_wei

http://www.his.com/~merkin/daoGloss.html

http://en.wikipedia.org/wiki/Heinrich_von_Kleist

Edward Slingerland / Effortless Action: Wu-wei As Conceptual Metaphor and Spiritual Ideal in Early China

[*7.91, *8.66]

fourfolds, Mathematics, Science, Space and Time

Noether’s Theorem

May 4, 2012 Martin K. Jones 6 Comments

Nature is thrifty in all its actions.

— Pierre Louis Maupertuis

From Wikipedia:

Noether’s (first) theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system’s behavior can be determined by the principle of least action.

Noether’s theorem can be stated informally:

If a system has a continuous symmetry property, then there are corresponding quantities whose values are conserved in time.

Note:

Symmetries are transformations or exchanges in space or time that leave systems structurally or functionally equivalent to what they were before. The equivalence may or may not be an identity, but only the same in appearance or behavior.

Conservation laws are equivalences for quantitative properties of systems. A given property of matter or energy is quantitatively the same before and after, or continuously through space or time. The functional measure of this property remains constant.

So consider an analogy between Noether’s Theorem and the concept of Equivalent Exchange: for (symmetrical, differentiable) exchanges, there are properties that are equivalent (conserved)!

http://en.wikipedia.org/wiki/Noether’s_theorem

http://en.wikipedia.org/wiki/Action_%28physics%29

http://en.wikipedia.org/wiki/Lagrangian

http://en.wikipedia.org/wiki/Principle_of_least_action

http://math.ucr.edu/home/baez/noether.html

fourfolds, Philosophy

Kant’s Reflective Perspectives on Experience

April 27, 2012 Martin K. Jones 2 Comments

The web site of Stephen R. Palmquist has a great wealth of material on fourfolds in relation to Kant’s as well as his own philosophy. From my own initial reading of his extensive material I have tried to choose a canonical Kantian fourfold which has the most relevance to my project.

The fourfold shown above Dr. Palmquist calls Kant’s “reflective perspectives on experience”. Consisting of the logical, the empirical, the transcendental, and the hypothetical, these facets bear a close analogical likeness to many of the fourfolds presented here.

Logical: Analytic a priori
Transcendental: Synthetic a priori
Hypothetical: Analytic a posteriori
Empirical: Synthetic a posteriori

Dr. Palmquist also has many of his own books available on his web site for the interested reader. I will certainly be returning to his web site in the future for much enjoyable study.

References:

http://www.hkbu.edu.hk/~ppp/

http://www.hkbu.edu.hk/~ppp/ksp2/KCR3.htm

[*7.68, *7.84]

fourfolds, linear logic, logic

The Four Binary Operators of Linear Logic

April 17, 2012 Martin K. Jones 14 Comments

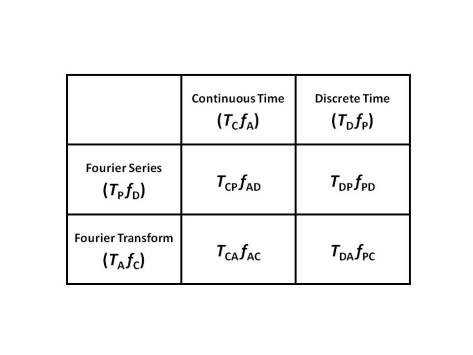
The four binary operators for Linear Logic can be described by their logical sequents, or inference rules (shown above in the table). Note that in the rules for the operators, the operator appears below and not above the horizontal line. Thus the sequents can be considered in two ways: moving from top to bottom, the operator is introduced, and moving from bottom to top, the operator is eliminated. As operators are introduced the rules deduce a formula containing instances of them, and as operators are eliminated the rules construct a proof of that formula without them. Also note that in the sequents the symbols A and B denote formula in our logic, and the symbols Γ and Δ are finite (possibly empty) sequences of formulae (but the order of the formulae do not matter), called contexts.

The rule for the operator & (with), additive conjunction, says that if A obtains along with the context Γ, and if B obtains also along with Γ, then A & B obtains along with Γ.

The rule for the operator ⊕ (plus), additive disjunction, says that if A obtains along with the context Γ, or if B obtains along with Γ, then A ⊕ B obtains along with Γ.

The rule for the operator ⅋ (par), multiplicative disjunction, says that if the combination A,B obtains along with the context Γ, then A ⅋ B obtains along with Γ.

The rule for the operator ⊗ (tensor), multiplicative conjunction, says that if A obtains along with context Γ, and if B obtains along with context Δ, then A ⊗ B obtains along with the combined context Γ,Δ.

There are several immediate observations we can make about these rules.

First, note that for operators & and ⅋, they are reversible. That is, if one obtains A & B or A ⅋ B, then one knows exactly what the previous step had to be to introduce the operator. In contrast, ⊕ and ⊗ are not reversible. If one has A ⊕ B, one doesn’t know if we started with A or with B. If one has A ⊗ B, one doesn’t know what was the context of A or what was the context of B.

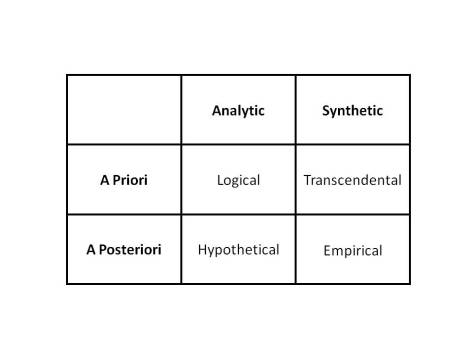
For this reason, I will consider & and ⅋ to be rational, and ⊕ and ⊗ to be empirical.

Second, note that all of the parts of the multiplicative sequents for ⅋ and ⊗ are the same above and below the horizontal line. In contrast, the parts of the additive sequents for & and ⊕ are different above and below the line. For &, a duplicated context is eliminated even as the operator is introduced. For ⊕, a new formula is introduced along with the introduction of the operator.

For this reason, I will consider & and ⊕ to be discrete, and ⅋ and ⊗ to be continuous.

References:

http://en.wikipedia.org/wiki/Sequent_calculus

http://en.wikipedia.org/wiki/Linear_logic

http://www.uni-obuda.hu/journal/Mihalyi_Novitzka_42.pdf

[*6.38, *6.40]

Computation, fourfolds, Space and Time

A Digital Universe

April 12, 2012 Martin K. Jones 1 Comment

A digital universe – whether 5 kilobytes or the entire Internet – consists of two species of bits: differences in space, and differences in time. Digital computers translate between these two forms of information – structure and sequence – according to definite rules. Bits that are embodied as structure (varying in space, invariant across time) we perceive as memory, and bits that are embodied as sequence (varying in time, invariant across space) we perceive as code. Gates are the intersections where bits span both worlds at the moments of transition from one instant to the next.